openMSE includes a set of functions, of class PM, for calculating Performance Metrics.
The available PM functions (referred to as PMs) can be found using the avail function:
avail("PM")## Searching for objects of class PM in package: MSEtool## Searching for objects of class PM in package: SAMtool## Searching for objects of class PM in package: DLMtool## [1] "AAVE" "AAVY" "LTY" "P10" "P100" "P50" "PNOF" "STY" "Yield"The PMs are used for summarizing the performance of the management procedures and plotting the results in trade-off plots.
Here we briefly describe the built-in Performance Metrics functions and demonstrate their use. In the next section we describe how users can develop their own PM methods.
Functions of class PM are used on an objects of class MSE, and return an object of class PMobj. Most of the time the PM functions are used internally in the summary or plotting functions, and it will not be necessary to access the PMobj directly.
To demonstrate the PM functions we first run a quick example MSE:
MSE <- runMSE()Overview of the PM Functions
We will use the P50 function to demonstrate the PM methods. Help documentation on the PM methods can be accessed in the usual way: either ?P50 in the R console or on the relevant page on the MSEtool function documentation site.
The P50 PM method calculates the probability that spawning biomass is above half of the spawning biomass that results in maximum sustainable yield \(\left(\text{SB} > 0.5\text{SB}_\text{MSY}\right)\).
Applying the P50 function to our MSE object results in the following output:
P50(MSE)## Spawning Biomass relative to SBMSY
## Prob. SB > 0.5 SBMSY (Years 1 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.04 0.80 0.98 0.92 0.98
## 2 0.14 1.00 1.00 1.00 1.00
## 3 0.96 0.88 1.00 1.00 1.00
##
## Mean
## [1] 0.38 0.89 0.99 0.97 0.99We can see that the PM function calculated, for the 6 MPs in the MSE object, the probability \(\text{SB} > 0.5\text{SB}_\text{MSY}\) for all 50 projection years.
The PM function prints out a summary table of the performance metrics statistics for the first 10 simulations and the last simulation (3 in this case) for each MP. The final line shows the overall probability of the performance metric, i.e the average performance across all simulations.
We will look into this output in a little more detail.
We can see that the first MP is curEref and the performance statistics for the first and second simulations are 0.04 and 0.14. How have these values been calculated and what do they mean?
Let’s first plot the spawning biomass relative to BMSY for the first two simulations of the AvC MP:
par(mfrow=c(1,2))
plot(1:MSE@proyears, MSE@SB_SBMSY[1,1,], type='l',
xlab="Years", ylab="SB/SBMSY", lwd=2, bty="l", ylim=c(0,2),
main="MP = 'AvC'; Sim = 1")
abline(h=0.5, lty=3)
plot(1:MSE@proyears, MSE@SB_SBMSY[2,1,], type='l',
xlab="Years", ylab='', lwd=2, bty="l", ylim=c(0,2),
main="MP = 'AvC'; Sim = 2")
abline(h=0.5, lty=3)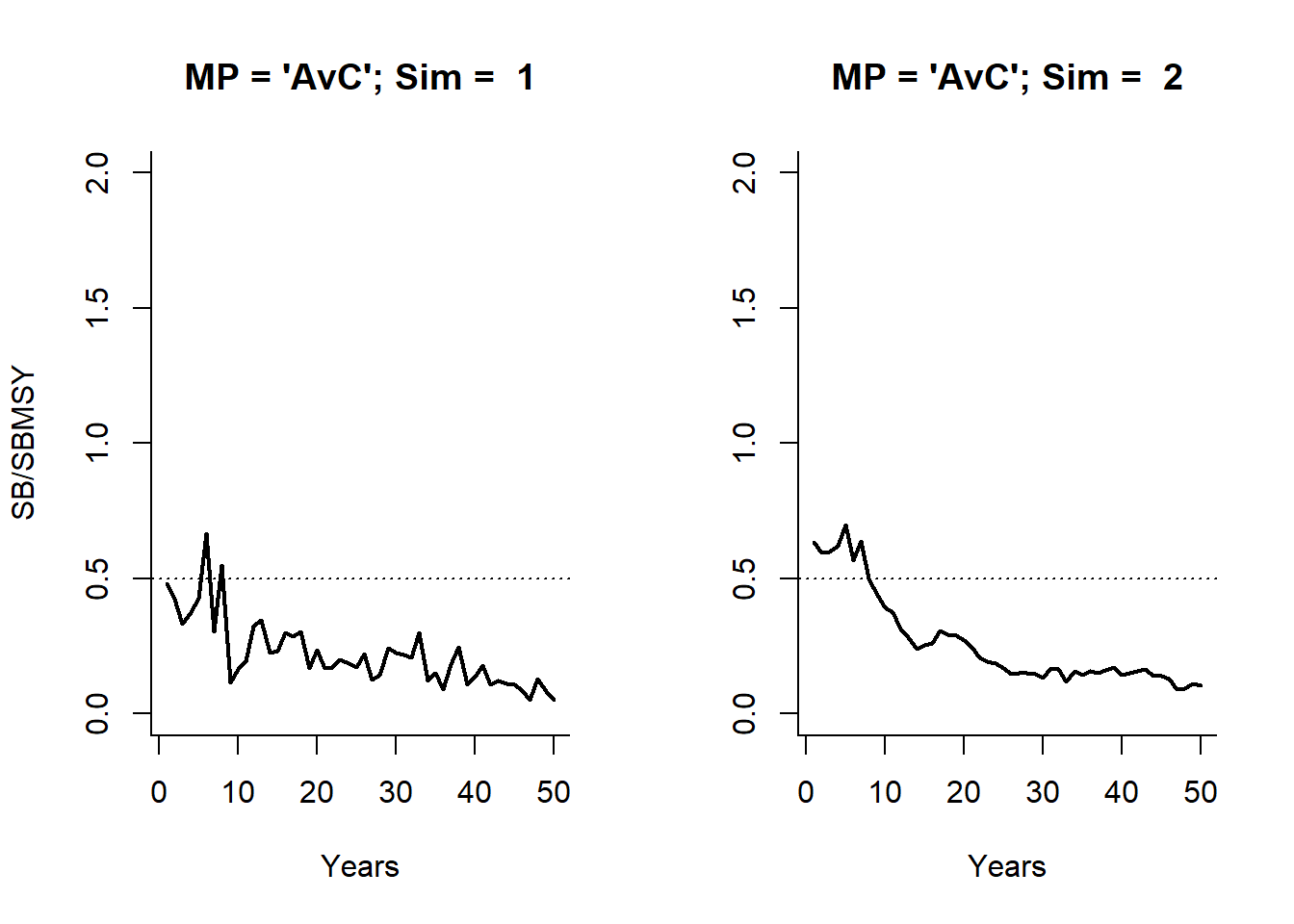
Now we will calculate fraction of years where spawning biomass is above 0.5 \(\text{SB}_\text{MSY}\) for the first and second simulations:
mean(MSE@SB_SBMSY[1,1,] > 0.5) # first simulation## [1] 0.04mean(MSE@SB_SBMSY[2,1,] > 0.5) # second simulation## [1] 0.14# identical to:
sum(MSE@SB_SBMSY[1,1,] > 0.5)/MSE@proyears## [1] 0.04sum(MSE@SB_SBMSY[2,1,] > 0.5)/MSE@proyears## [1] 0.14Notice how the performance statistics for each simulation correspond with the plot shown above?
The overall performance is then calculated by the probability over all simulations, i.e for the first MP curEref:
mean(MSE@SB_SBMSY[,1,]>0.5)## [1] 0.38And for 5 MPs:
round(apply(MSE@SB_SBMSY >0.5, 2, mean),2)## [1] 0.38 0.89 0.99 0.97 0.99which, reassuringly, is the same as the output of the P50 function.
Customizing the PM Functions
The PM functions allow for very quick calculation of performance metrics. For example, suppose that instead of calculating performance over all projection years, we are only interested in the long-term performance, say over the last 10 years. This can be easily achieved using the Yrs argument in the PM function:
P50(MSE, Yrs=c(41,50))## Spawning Biomass relative to SBMSY
## Prob. SB > 0.5 SBMSY (Years 41 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.0 1.0 1 1 1
## 2 0.0 1.0 1 1 1
## 3 0.9 0.9 1 1 1
##
## Mean
## [1] 0.30 0.97 1.00 1.00 1.00Or the first 10 years:
P50(MSE, Yrs=c(1,10))## Spawning Biomass relative to SBMSY
## Prob. SB > 0.5 SBMSY (Years 1 - 10)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.2 0.3 0.9 0.6 0.9
## 2 0.7 1.0 1.0 1.0 1.0
## 3 0.9 0.8 1.0 1.0 1.0
##
## Mean
## [1] 0.60 0.70 0.97 0.87 0.97The other biomass Performance Metric functions work in the same way:
P10(MSE) # probability SB > 0.1SB_MSY for all years## Spawning Biomass relative to SBMSY
## Prob. SB > 0.1 SBMSY (Years 1 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.90 1 1 1 1
## 2 0.96 1 1 1 1
## 3 1.00 1 1 1 1
##
## Mean
## [1] 0.95 1.00 1.00 1.00 1.00P100(MSE) # probability SB > SB_MSY for all years## Spawning Biomass relative to SBMSY
## Prob. SB > SBMSY (Years 1 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.00 0.24 0.82 0.64 0.92
## 2 0.00 0.40 0.94 0.94 0.96
## 3 0.38 0.26 0.86 0.58 0.96
##
## Mean
## [1] 0.13 0.30 0.87 0.72 0.95Long-term, short-term and overall average yield are calculated using LTY, STY and Yield respectively:
LTY(MSE)## Average Yield relative to Reference Yield (Years 41-50)
## Prob. Yield > 0.5 Ref. Yield (Years 41-50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.2 1 1 1 0
## 2 0.4 1 1 1 0
## 3 1.0 1 1 1 0
##
## Mean
## [1] 0.53 1.00 1.00 1.00 0.00STY(MSE)## Average Yield relative to Reference Yield (Years 1-10)
## Prob. Yield > 0.5 Ref. Yield (Years 1-10)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.8 0.6 0.3 0.5 0
## 2 1.0 1.0 0.9 1.0 0
## 3 1.0 1.0 0.9 1.0 0
##
## Mean
## [1] 0.93 0.87 0.70 0.83 0.00Yield(MSE)## Yield relative to Reference Yield (Years 1-50)
## Mean Relative Yield (Years 1-50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.55 0.83 0.74 0.83 0
## 2 0.77 1.07 0.86 1.01 0
## 3 1.20 1.18 0.98 1.15 0
##
## Mean
## [1] 0.84 1.03 0.86 1.00 0.00The PNOF PM function calculates the probability of not overfishing:
PNOF(MSE)## Probability of not overfishing (F<FMSY)
## Prob. F < FMSY (Years 1 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0.00 0.42 1 0.78 1
## 2 0.00 0.54 1 0.98 1
## 3 0.66 0.54 1 0.90 1
##
## Mean
## [1] 0.22 0.50 1.00 0.89 1.00Finally, the average annual variability in yield (AAVY) can be calculated with the AAVY function:
AAVY(MSE)## Average Annual Variability in Yield (Years 1-50)
## Prob. AAVY < 20% (Years 1-50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0 0 0 0 0
## 2 1 1 1 1 1
## 3 0 0 0 0 0
##
## Mean
## [1] 0.33 0.33 0.33 0.33 0.33By default the AAVY PM function calculates the probability that AAVY is less than 20%. This reference level can easily be modified using the Ref argument:
AAVY(MSE, Ref=0.15) # prob. AAVY < 15%## Average Annual Variability in Yield (Years 1-50)
## Prob. AAVY < 15% (Years 1-50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 0 0 0 0 0
## 2 1 1 1 1 1
## 3 0 0 0 0 0
##
## Mean
## [1] 0.33 0.33 0.33 0.33 0.33AAVY(MSE, Ref=0.30) # prob. AAVY < 30%## Average Annual Variability in Yield (Years 1-50)
## Prob. AAVY < 30% (Years 1-50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 1 1 1 1 1
## 2 1 1 1 1 1
## 3 1 1 1 1 1
##
## Mean
## [1] 1 1 1 1 1The other PM functions also have the Ref argument which can be used in the same way. For example, you may notice that the P50 and P100 functions are identical except for the value of the Ref argument:
args(P50)## function (MSEobj = NULL, Ref = 0.5, Yrs = NULL)
## NULLargs(P100)## function (MSEobj = NULL, Ref = 1, Yrs = NULL)
## NULLIt follows then that it is very simple to calculate a custom performance metric based on the built-in PM functions. For example, suppose we wanted to calculate the probability that spawning biomass was above 5% of BMSY. This can be achieved by using any of the biomass-based PM functions and modifying the Ref argument:
P50(MSE, Ref=0.05)## Spawning Biomass relative to SBMSY
## Prob. SB > 0.05 SBMSY (Years 1 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 1 1 1 1 1
## 2 1 1 1 1 1
## 3 1 1 1 1 1
##
## Mean
## [1] 1 1 1 1 1P100(MSE, Ref=0.05)## Spawning Biomass relative to SBMSY
## Prob. SB > 0.05 SBMSY (Years 1 - 50)
## curEref FMSYref FMSYref50 FMSYref75 NFref
## 1 1 1 1 1 1
## 2 1 1 1 1 1
## 3 1 1 1 1 1
##
## Mean
## [1] 1 1 1 1 1More information on customizing PM functions can be found in the Custom Performance Metrics section.