Length-based selectivity

For flat-topped selectivity in block \(b\), two parameters are used and expressed in terms of length units: the length of 5% selectivity (\(L^5_b\)) and the length of full selectivity \(L^{\textrm{FS}}_b\).

For dome selectivity, a third parameter, the selectivity at \(L_{\infty}\), \(V^{L_{\infty}}_b\) is also used.

The selectivity \(v\) at length \(L\) at the midpoint of length bin \(\ell\) in year \(y\) for block \(b\) is:

\[ v_{y,\ell,b} = \begin{cases} 2^{-[(L'_\ell - L^{\textrm{FS}}_b)/(\sigma^{\textrm{asc}}_b)]^2} & \textrm{if } L'_\ell < L^{\textrm{FS}}_b\\ 1 & \textrm{if logistic and } L'_\ell \ge L^{\textrm{FS}}_b,\\ 2^{-[(L'_\ell - L^{\textrm{FS}}_b)/(\sigma^{\textrm{des}}_b)]^2} & \textrm{if dome and } L'_\ell \ge L^{\textrm{FS}}_b \end{cases} \]

where \(\sigma^{\textrm{asc}}_b = (L^5_b - L^{\textrm{FS}}_b)/\sqrt{-\log_2(0.05)}\) and \(\sigma^{\textrm{des}}_b = (L_{\infty} - L^{\textrm{FS}}_b)/\sqrt{-\log_2(V^{L_{\infty}}_b)}\) control the shape of the ascending and descending limbs, respectively, of the selectivity function.

Length-based selectivity is converted to age-based selectivity in the age-structured model as:

\[ v_{y,a,b} = \sum_\ell v_{y,\ell,b} P(\ell|a)_y \]

where \(P(\ell|a)_y\) is the probability of length-at-age, which can be time-varying:

\[ P(\ell|a)_y = \begin{cases} \phi_y(L'_{\ell+1}) & \ell = 1\\ \phi_y(L'_{\ell+1}) - \phi_y(L'_\ell) & \ell = 2, \ldots, L - 1,\\ 1 -\phi_y(L'_\ell) & \ell = L \end{cases} \]

and \(\phi_y(L'_{\ell})\) is the cumulative normal distribution function with mean length at age \(L_{y,a}\) and standard deviation \(\sigma^L_{y,a}\) evaluated at \(L'_{\ell}\) which is the lower boundary of length bin \(\ell\).

Age-based selectivity

Parametric functions can be directly specified in terms of age, where

\[ v_{y,a,b} = \begin{cases} 2^{-[(a - a^{\textrm{FS}}_b)/(\sigma^{\textrm{asc}}_b)]^2} & \textrm{if } a < a^{\textrm{FS}}_b\\ 1 & \textrm{if logistic and } a \ge a^{\textrm{FS}}_b,\\ 2^{-[(a - a^{\textrm{FS}}_b)/(\sigma^{\textrm{des}}_b)]^2} & \textrm{if dome and } a \ge a^{\textrm{FS}}_b \end{cases} \]

where \(a^{\textrm{FS}}_b\) is the age of full selectivity, \(\sigma^{\textrm{asc}}_b = (a^5_b - a^{\textrm{FS}}_b)/\sqrt{-\log_2(0.05)}\), \(\sigma^{\textrm{des}}_b = (A - a^{\textrm{FS}}_b)/\sqrt{-\log_2(V^A_b)}\) with \(a^5_b\) the age of 5 percent selectivity, and \(V^A_b\) is the selectivity at the maximum age.

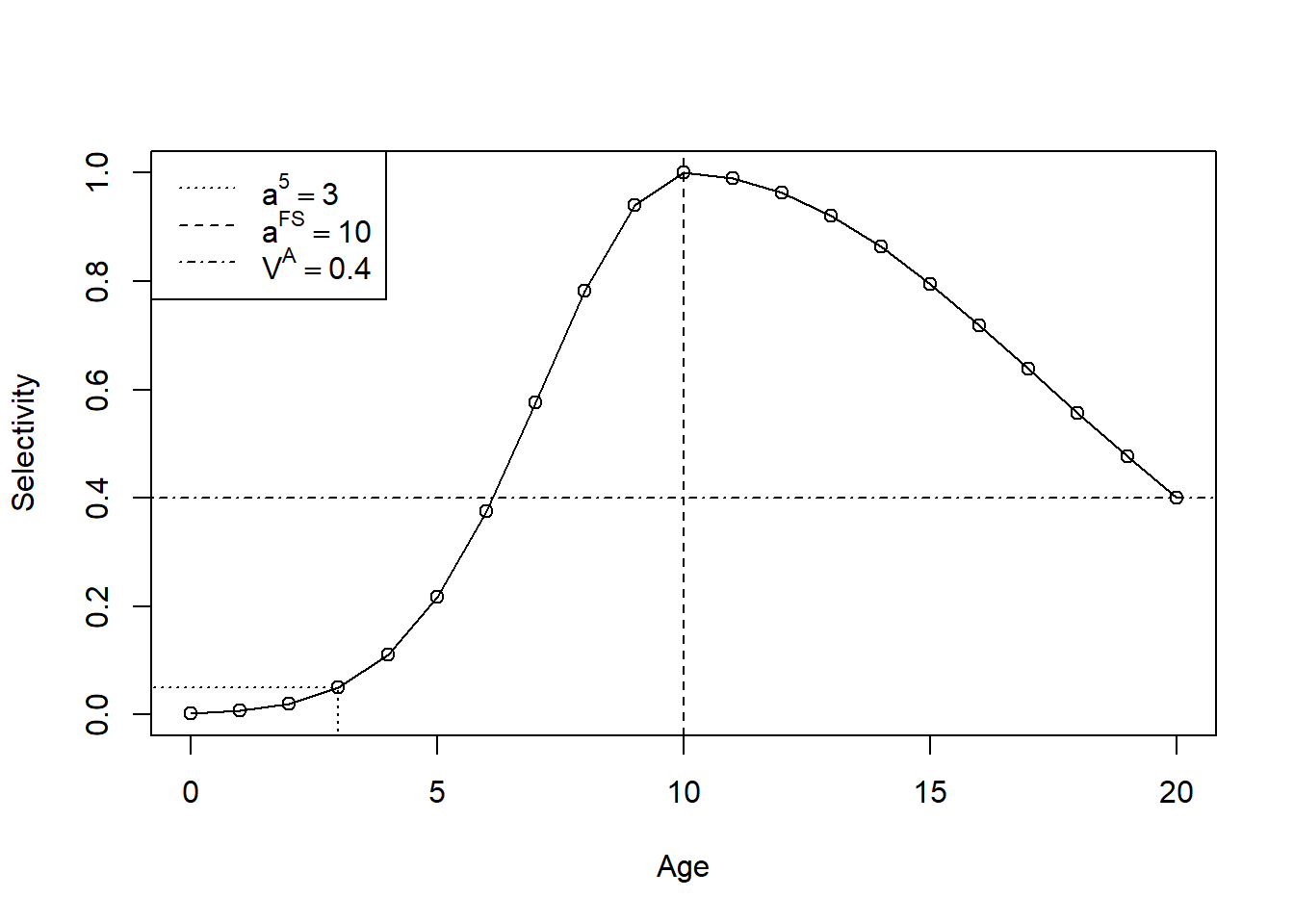
Figure 1: Example age-based selectivity function.

Selectivity can also be parameterized where \(v_{y,a,b}\) are free independent parameters. In this case, selectivity does not vary among years.

Total mortality \(Z\) in year \(y\) and for age \(a\) is the sum of fishing mortality \(F\) from all fleets and natural mortality \(M\),

\[ Z_{y,a} = M_{y,a} + \sum_f v_{y,a,f} F_{y,f},\]

where \(v_{y,a,f}\) is the fleet selectivity after assigning blocks to fleets.