Total objective function

The total objective function \(\textrm{LL}\) to be maximized is \[\textrm{LL} = \sum_{i=1}^9\Lambda_i + \sum \textrm{pr} + \sum_y\sum_f\textrm{pen}_{y,f},\]

including the log likelihoods \(\Lambda_i\), logarithm of the parameter priors \(pr\), and penalty functions, described below.

Likelihoods

If the model is conditioned on catch and fishing mortality rates are estimated parameters, then the log-likelihood component \(\Lambda_1\) of the catch is \[\Lambda_1 = \sum_f \left[\lambda^{Y}_f \sum_y \left(-\log(\omega_{y,f}) - \dfrac{[\log(Y^{\textrm{obs}}_{y,f}) - \log(Y^{\textrm{pred}}_{y,f})]^2}{2 \omega _{y,f}^2}\right)\right],\]

where \(\textrm{obs}\) and \(\textrm{pred}\) indicate observed and predicted quantities, respectively, \(\lambda\) are likelihood weights, and \(\omega\) is the catch standard deviation. With a small standard deviation for the catch likelihood relative to the variance in other likelihood components, i.e., \(\omega = 0.01\), the predicted catch should match the observed catch in the model.

The log-likelihood component \(\Lambda_2\) of survey data is \[\Lambda_2 = \sum_s \left[ \lambda^I_s \sum_y \left(-\log(\sigma_{y,s}) - \dfrac{[\log(I^{\textrm{obs}}_{y,s}) - \log(I^{\textrm{pred}}_{y,s})]^2}{2\sigma_{y,s}^2}\right) \right].\]

The log-likelihood component \(\Lambda_3\) of catch-at-age data is \[\Lambda_3 = \sum_f \lambda^A_f \left[\sum_y O^A_{y,f} \sum_a p^{\textrm{obs}}_{y,a,f} \log(p^{\textrm{pred}}_{y,a,f})\right],\] where \(O^A\) is the annual sample sizes for the age compositions.

The log-likelihood component \(\Lambda_4\) of catch-at-length data is \[\Lambda_4 = \sum_f \lambda^L_f \left[ \sum_y O^L_{y,f} \sum_{\ell} p^{\textrm{obs}}_{y,\ell,f} \log(p^{\textrm{pred}}_{y,\ell,f})\right]\] where \(O^L\) is the annual sample sizes for the length compositions.

The log-likelihood component \(\Lambda_5\) for the observed mean size in this catch is:

\[\Lambda_5 = \sum_f \lambda^{\bar{L}}_f\left[ \sum_y \left(-\log(\eta_{y,f}) - \dfrac{[\bar{L}^{\textrm{obs}}_{y,f} - \bar{L}^{\textrm{pred}}_{y,f}]^2}{2 \eta^2_{y,f}}\right)\right],\] for mean lengths, or

\[\Lambda_5 = \sum_f \lambda^{\bar{w}}_f\left[ \sum_y \left(-\log(\eta_{y,f}) - \dfrac{[\bar{w}^{\textrm{obs}}_{y,f} - \bar{w}^{\textrm{pred}}_{y,f}]^2}{2 \eta^2_{y,f}}\right)\right],\] for mean weights, where \(\eta_{y,f}\) is the standard deviation of the mean size. With constant coefficient of variation (CV), \(\eta_{y,f} = \bar{w}^{\textrm{obs}}_{y,f} CV^{\eta}_f\).

The log-likelihood component \(\Lambda_6\) of annual estimated recruitment deviates \(\delta_y\) in log space is \[\Lambda_6 = \Sigma_y\left(-\log(\tau) - \dfrac{\delta_y^2}{2 \tau^2}\right),\] where \(\tau\) is the standard deviation of recruitment deviates.

The log-likelihood component \(\Lambda_7\) of the equilibrium catch is \[\Lambda_7 = \sum_f \lambda^{Y}_f \left(-\log(\omega^{\textrm{eq}}_f) - \dfrac{[\log(Y^{\textrm{eq,obs}}_f) - \log(Y^{\textrm{eq,pred}}_f)]^2}{2 \times (\omega^{\textrm{eq}}_f)^2}\right),\]

The log-likelihood component \(\Lambda_8\) of the survey proportion-at-age data is \[\Lambda_8 = \sum_s \lambda^{IA}_s \left[\sum_y O^{IA}_{y,s} \sum_a p^{\textrm{obs}}_{y,a,s} \log(p^{\textrm{pred}}_{y,a,s})\right],\] where \(O^{IA}\) is the annual sample sizes for the survey age compositions.

The log-likelihood component \(\Lambda_9\) of the survey proportion-at-length data is \[\Lambda_9 = \sum_s \lambda^{IL}_s \left[ \sum_y O^{IL}_{y,s} \sum_{\ell} p^{\textrm{obs}}_{y,\ell,s} \log(p^{\textrm{pred}}_{y,\ell,s})\right]\] where \(O^{IL}\) is the annual sample sizes for the survey length compositions.

Priors

Vague priors are added to selectivity parameters to aid in convergence, with \[ \begin{align} x^{\textrm{LFS}}_b &\sim N(0,3)\\ \textrm{logit}^{-1}(x^{\textrm{L5}}_b) &\sim \textrm{Beta}(1.01, 1.01)\\ V^{L_{\infty}}_b &\sim \textrm{Beta}(1.01, 1.01) \end{align}\]

If free selectivity parameters are estimated, then \[v_{y,a,f} \sim \textrm{Beta}(1.01, 1.01)\]

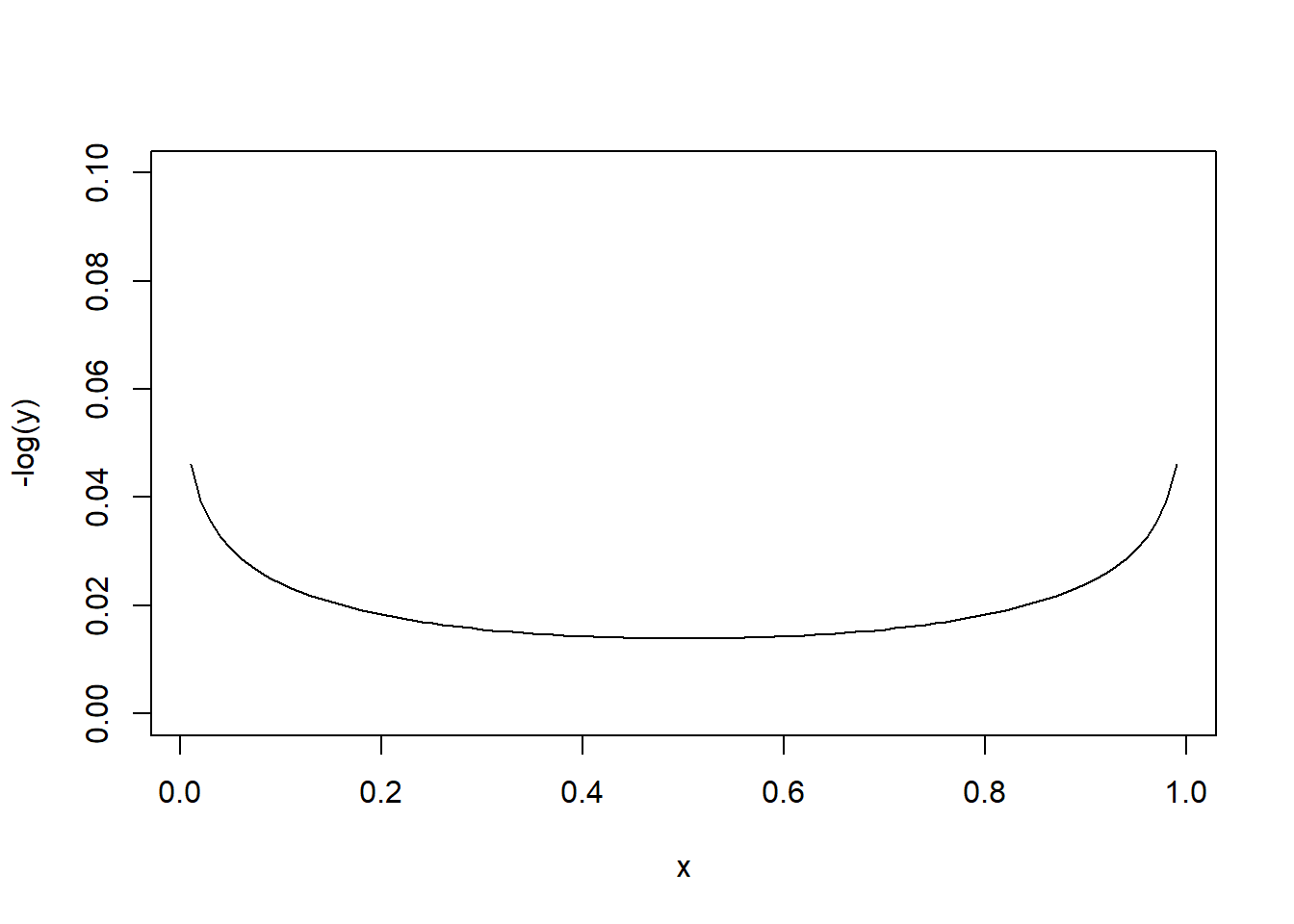
Figure 1: Beta prior for aiding convergence with constants removed where x is the parameter and y is the prior density evaluated at x.

Optional priors

See sub-article on priors.

Penalties

A penalty to the likelihood is added when \(F_{y,f} \ge F_{\textrm{max}}\) for any year and fleet. The penalty is

\[\textrm{pen}_{y,f} = \begin{cases} 0.01 (F_{y,f} - F_{\textrm{max}})^2 & F_{y,f} \ge F_{\textrm{max}}\\ 0 & \textrm{otherwise} \end{cases}.\]